Miło mi Cię powitać w mojej zacisznej krainie
Mam nadzieję że przyjemnie spędzisz tutaj czas
witam w ustronnym zakątku
odrobinę eklektyczna witryna indywidualna
Miło mi Cię powitać w mojej zacisznej krainie
Mam nadzieję że przyjemnie spędzisz tutaj czas
odrobinę eklektyczna witryna indywidualna
W tym miejscu dzielę się garstką wspomnień prezentując kilka projektów, które pochodzą jeszcze z okresu świetności komputerów 8-bitowych. Tworzą rodzaj pamiętnika z ekscytującego zajęcia konstruowania i uruchamiania układów. Wszystkie widoczne prace to radosna twórczość, efekt inspirującej fascynacji elektronką. Zamieszczam fotografie wraz z krótkim opisem, ewentualnie dodatkowymi detalami technicznymi. Przyznaję że zgłębianie tajników elektroniki jest jak przygoda, to niezwykle ciekawe i wciągające zajęcie.
Ośmiobitowy mikrokomputer CA80, a właściwie mikroprocesorowy sterownik czasu rzeczywistego do sterowania i kontroli urządzeń.
Przez dość długi okres włączony w trybie 24-godzinnym pełnił funkcje automatyki do akwarium.
(sterowanie oświetleniem, natlenianie wody)
na poniższej prezentacji uruchomiony CA80 - pomimo upływu lat nadal jest sprawny
Tester stanów logicznych w standardzie TTL - wykonany na układzie CMOS
wskazuje wysoki lub niski poziom logiczny ewentualnie obecność zmiennego sygnału cyfrowego.
Na ostatnim zdjęciu umieściłem najstarszy zachowany układ, monofoniczny wzmacniacz audio małej mocy.
Korektor graficzny audio, oparty wyłącznie na tranzystorach, bez użycia układów scalonych.
Skonstruowany do współpracy z "wieżą typu midi". Zapewniał dziesięcio-punktową korekcję barwy dźwięku.
central processor unit
Komputer CA80 funkcjonuje w oparciu o mikroprocesor Z80 A CPU, "prawdziwe cudeńko"jak z sentymentem zwykłem określać ten niezwykle wdzięczny układ
poglądowe dane i podstawowy opis funkcjonowania mikroprocesora Z80
Mikroprocesor to układ scalony, którego działalność polega na wykonywaniu ciągu rozkazów (tworzących program) umieszczonych w pamięci zewnętrznej w takt impulsów zegarowych. Obsługiwany zestaw instrukcji umożliwia przesyłanie danych oraz wykonywanie różnych operacji arytmetycznych i logicznych na rejestrach mikroprocesora, pamięci i portach wejścia / wyjścia. Rozkazy są reprezentowane jako ośmiobitowe liczby binarne, kody maszynowe rozkazów mają długość od 1 do 4 bajtów, a każdy rozkaz jest złożeniem od 1 do 6 cykli maszynowych tworzących cykl rozkazowy (cykl instrukcji).
Komunikacja mikroprocesora z pamięcią i portami wejścia / wyjścia odbywa się poprzez 5 cykli maszynowych.
Każdy cykl maszynowy trwa od 3 do 6 taktów (okresów) zegara Ø.
Po włączeniu układu następuje automatyczne zerowanie mikroprocesora, przy pomocy wejścia zerującego RESET (aktywny niski poziom logiczny), które powoduje:
Mikroprocesor pobiera przy pomocy cyklu OCF z komórki pamięci o adresie 0000H kod pierwszego rozkazu do wykonania.
Podczas ciągłej pracy stan linii RESET jest sprawdzany wraz z każdym narastającym zboczem zegara Ø.
| REJESTRY | |
|---|---|
| PC | licznik rozkazów (wskazuje adres aktualnego rozkazu) |
| SP | wskaźnik stosu (wskazuje aktualny adres wierzchołka stosu) |
| B, C, D, E, H, L | rejestry ogólnego przeznaczenia |
| A | akumulator (do wykonywania operacji arytmetyczno logicznych) |
| F | wskaźniki sygnalizacyjne (do wykonywania operacji arytmetycznych i logicznych) |
| R | adres odświeżania pamięci ( wystawiany na A0 - A7 w każdym cyklu OCF) |
| I | bardziej znaczący bajt adresu procedury obsługującej przerwanie INT ( TRYB 2) |
| IX, IY | rejestry indeksowe |
| WYPROWADZENIA | |
|---|---|
| A0 - A15 | 16-bitowa magistrala adresowa |
| D0 - D7 | 8-bitowa magistrala danych |
| MREQ | linia żądania dostępu do pamięci |
| IORQ | linia żądania dostępu do portów wejścia/wyjścia |
| RD | sygnał sterujący odczytem (pamięć lub porty we/wy) |
| WR | sygnał sterujący zapisem (pamięć lub porty we/wy) |
| M1 | sygnalizuje pobieranie kodu rozkazu |
| NMI | linia zgłaszanie przerwania niemaskowalnego |
| INT | linia zgłaszanie przerwania maskowalnego |
| HALT | sygnał synalizujący stan halt mikroprocesora |
| RESET | linia zerowania mikroprocesora |
| WAIT | wstawianie taktów oczekiwania (przedłużenie operacji odczytu lub zapisu) |
| BUSRQ | żądanie układu DMA dostępu do magistral i sygnałów sterujących |
| BUSAK | potwierdzenie stanu odcięcia magistral i sygnałów sterujących |

OCF - cykl pobrania kodu rozkazu
OCF - cykl pobrania kodu rozkazu
Na początku taktu T1 mikroprocesor wystawia na magistralę adresową (linie A0 – A15) zawartość licznika rozkazów PC (będącą adresem komórki pamięci którą chce odczytać). Operacja odczytu kodu rozkazu rozpoczyna się w połowie taktu T1 wraz z uaktywnieniem sygnałów MREQ i RD. Podczas opadającego zbocza taktu T2 testowana jest linia WAIT – jeżeli (dopóki ) jest aktywna to między takty T2 a T3 wstawiane są takty oczekiwania Tw. Stabilna dana z pamięci (kod rozkazu) musi być ustawiona na magistrali danych (linie D0 – D7) przed narastającym zboczem zegara rozpoczynającym takt T3.

MR - cykl odczytu z pamięci
MW - cykl zapisu do pamięci
MR - cykl odczytu z pamięci
Na początku taktu T1 mikroprocesor wystawia adres komórki pamięci którą chce odczytać (zawartość licznika rozkazów PC na liniach A0 – A15). Wraz z opadającym zboczem zegara w tym samym takcie T1 uaktywnia sygnały sterujące odczytem MREQ i RD. Stabilna informacja z pamięci musi się pojawić na magistrali danych (linie D0 – D7) tuż przed opadającym zboczem zegara w takcie T3.
MW - cykl zapisu do pamięci
Na początku taktu T1 zostaje ustawiony adres (zawartość licznika rozkazów PC na liniach A0 – A15) komórki pamięci na której ma być dokonana operacja zapisu. Wraz z opadającym zboczem zegara w tym samym takcie T1 uaktywniany jest sygnał MREQ a na magistrale danych (linie D0 – D7) wystawiana jest ośmiobitowa liczba binarna która ma być zapisana do pamięci. Oeracja zapisu zostanie dokonana wraz z narastającym zboczem sygnału WR.
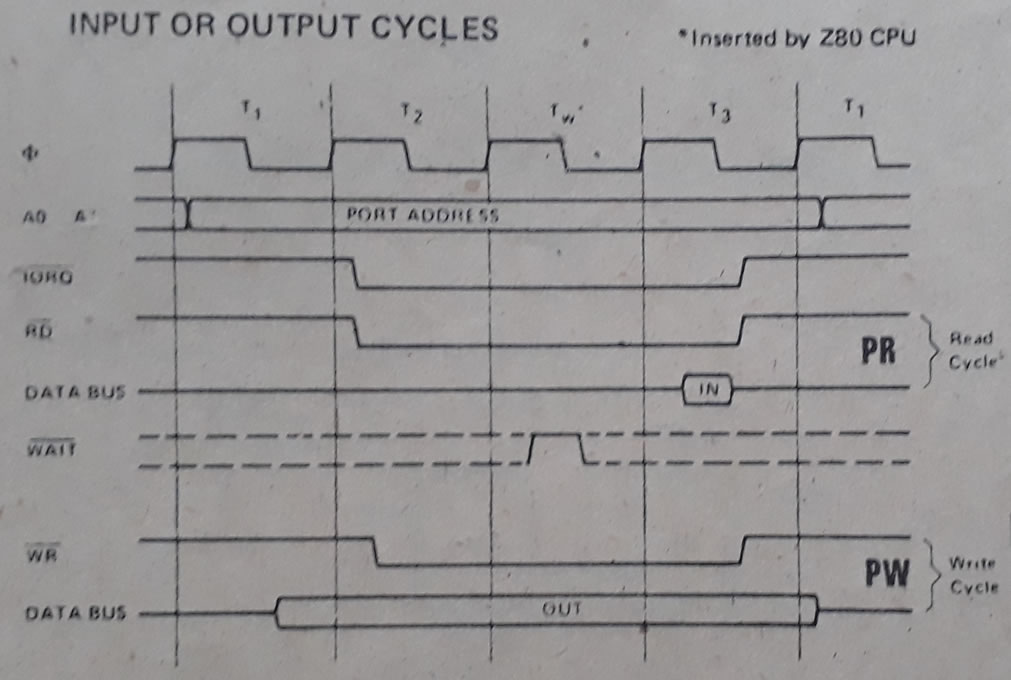
PR - cykl odczytu z z portu wejściowego
PW - cykl zapisu do do portu wyjściowego
PR - cykl odczytu z z portu wejściowego
Na początku taktu T1 mikroprocesor wystawia mniej znaczący bajt magistrali adresowej (A0 - A7), będący adresem portu wejściowego. Dalej na początku taktu T2 uaktywniane są sygnały sterujące odczytem IORQ i RD. Stabilna informacja na magistrali danych (linie D0 – D7) pochodząca z portu wejściowego musi pojawić się przed opadającym zboczem zegara w takcie T3
PW - cykl zapisu do do portu wyjściowego
Na początku taktu T1 mikroprocesor wystawia mniej znaczący bajt magistrali adresowej (A0 - A7), będący adresem portu wyjściowego. Wraz z opadającym zboczem zegara w takcie T1 na magistralę danych (linie D0 – D7) wystawiana jest ośmiobitowa liczba binarna w celu zapisania do portu wyjściowego. Sygnały sterujące zapisem IORQ i WR zostają uaktywnione na początku taktu T2. Zapis danej do portu wyjściowego następuje wraz z narastającym zboczem sygnału WR.

PRZYKŁADOWY CYKL ROZKAZOWY
dotyczy rozkazu LD (HL),n
Każdy rozkaz mikroprocesora Z80 jest złożeniem od 1 do 6 cykli maszynowych (OCF, MR, MW, PR, PW) składających się na rozkaz.
Kody maszynowe rozkazów mogą być:
jedno, dwu, trzy i cztero - bajtowe.
Cykl maszynowy M1 jest zawsze cyklem pobrania kodu rozkazu.
Jeśli rozkaz jest wielobajtowy to mikroprocesor najpierw pobiera wszystkie bajty rozkazu, po czym przystępuje do jego wykonania.
Jeżeli rozkaz traktuje dwie kolejne koórki pamięci jako jedną 16-to bitową liczbę binarną, to mniej znaczący bajt tej liczby umieszczony jest w komórce pamięci o niższym adresie.
Z80 pozwala na przyjęcie i obsługę dwóch rodzajów przerwań:
Stan obu linii zgłaszania przerwań testowany jest na końcu wykonywania każdego rozkazu wraz z narastającym zboczem ostatniego taktu cyklu rozkazowego (z wyjątkiem rozkazów EI i DI stan linii przerwań na końcu tych rozkazów nie jest sprawdzany).
Pierwsza jest sprawdzana linia NMI, następnie linia INT (pod warunkiem że rejestr IFF1=1 odblokowany system przerwań maskowalnych).
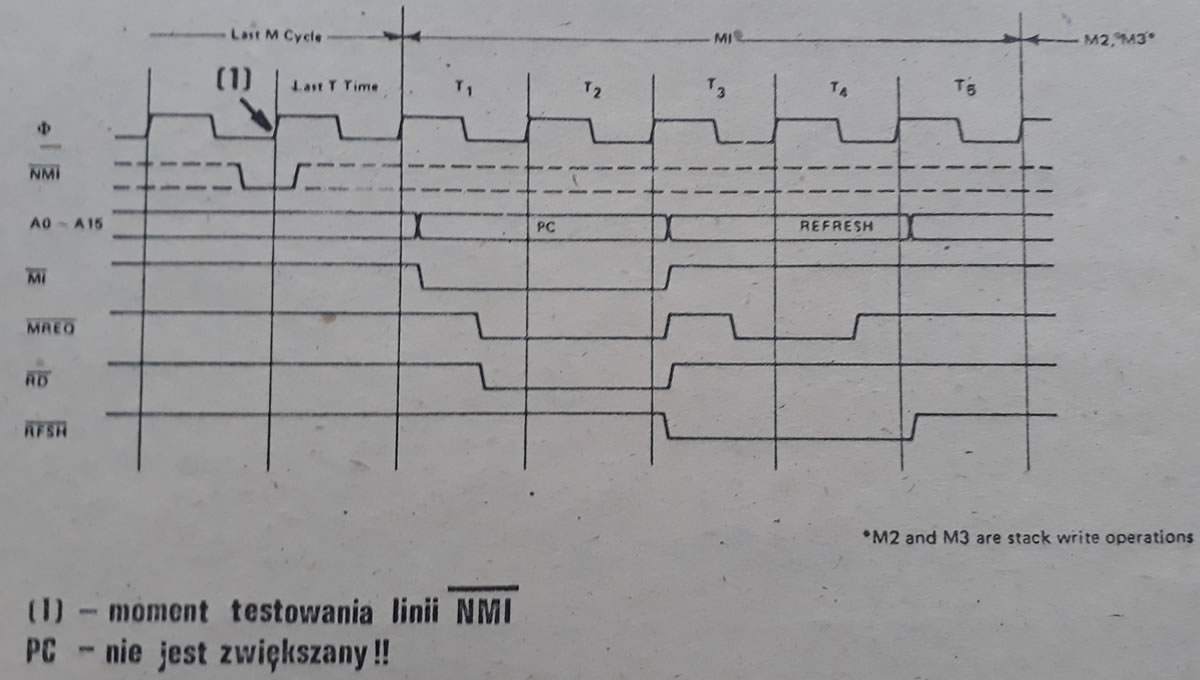
Wykres Czasowy - przyjęcie przerwania niemaskowalnego NMI
Zgłoszenie przerwania na wejściu przerywającym NMI spowoduje :
schowanie na stos aktualnej zawartości
licznika programu (PC)
(SP-1) ‹-- PCH | (SP-2) ‹-- PCL | SP ‹-- SP-2
Mikroprocesor przyjmując przerwanie NMI wykonuje kolejno:
Przerwanie NMI można rozumieć jako wymuszony zewnętrznie rozkaz CALL 66H
Procedura obsługi przerwania NMI powinna zostać zakończona rozkazem RETN – powrót z procedury obsługi przerwania niemaskowalnego, gdzie wykonywane jest odtworzenie stanu rejestru IFF1 (IFF1 ‹-- IFF2) sprzed przerwania NMI
Z80 umożliwia 3 sposoby przyjęcia przerwania maskowalnego INT:
Zmiany trybu dokonujemy przy pomocy rozkazów:
Przyjęcie przerwania maskowalnego jest możliwe pod warunkiem że system przerwań jest odblokowany, rejestr IFF1=1.
blokowania / odblokowania systemu przerwań dokonujemy za pomocą rozkazów:
Przyjęcie przerwania niezależnie od trybu powoduje wyzerowanie rejestrów IFF1 i IFF2
RETI to ostatni rozkaz kończący procedurę obsługi przerwania maskowalnego.

Wykres Czasowy - przyjęcie przerwania maskowalnego INT
TRYB 0 | TRYB 1
TRYB 0
urządzenie zewnętrzne zgłaszające przerwanie musi dostarczyć kod rozkazu do wykonania.
najczęściej jest to rozkaz RSTp, lub CALLnn
cykl maszynowy INTA rozpoczyna przyjęcie przerwania:
TRYB 1
Przyjęcie i obsługa przerwania takie jak w Trybie 0 z tym że wewnętrznie zostaje wymuszone wykonanie rozkazu RST38H

Wykres Czasowy - przyjęcie przerwania maskowalnego INT
TRYB 2
TRYB 2
cykl maszynowy INTA rozpoczyna przyjęcie przerwania, urządzenie zewnętrzne zgłaszające przerwanie dostarcza WEKTOR PRZERWAŃ (ośmiobitowa liczba binarna, gdzie bit D0 = 0 zawsze), który jest dołączany do zawartości rejestru I, tworząc szesnastobitowy adres pod którym jest przechowywany adres procedury obsługującej przerwanie. Zawartość licznika rozkazów PC chowana jest na stos, następnie wykonywany jest skok do procedury obsługującej przerwanie.
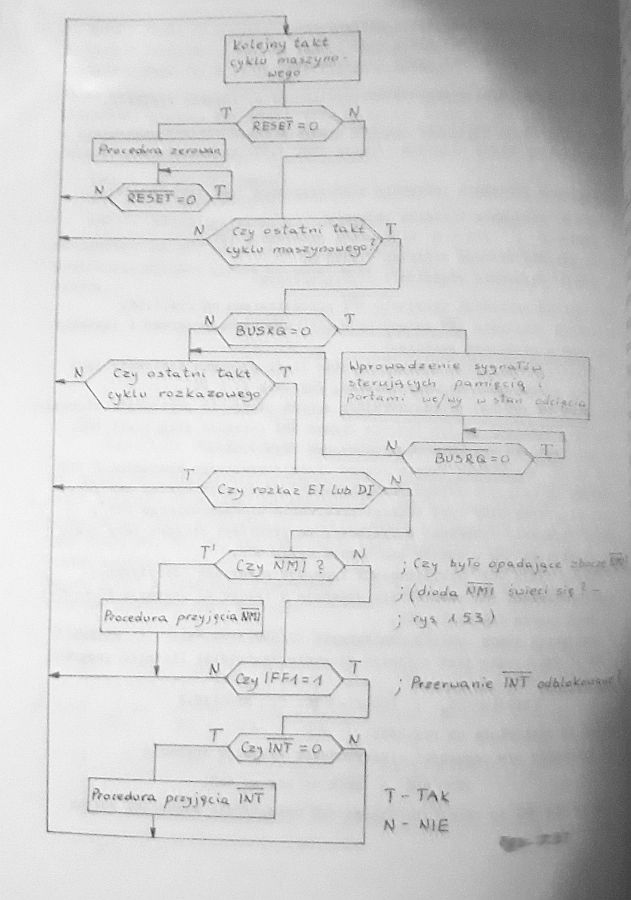
wraz z każdym narastającym zboczem zegara Ø, mikroprocesor Z80 pracuje zgodnie z powyższym algorytmem
Na początku każdego taktu zegara Ø, sprawdzany jest stan następujących wejść sterujących:
Wykonywane czynności ściśle zależą od aktualnego stanu wejść sterujących mikroprocesora oraz czy nowy cykl zegara jest:
Następnie sprawdzana jest aktywność wejść systemu przerwań, kolejno:
Przerwania:
do oszacowania poboru energii elektrycznej i przybliżonych kosztów użytkowania urządzeń.
OBLICZ
Przybliżony Koszt Zużycia Energii Elektrycznej
dzień
zużycie kW/h
koszt zł
miesiąć
zużycie kw/h
koszt zł
rok
zużycie kw/h
koszt zł
cennik taryf rozliczeniowych zł za zużycie 1kW/h
( szacunkowe cenny brutto zawierają 5% VAT według cennika PGE obowiązującego od września 2022 w woj. podlaskim )
taryfy jednostrefowe całodobowe:

Multimetry oraz garstka pozostałych elementów elektronicznych wraz z kilkoma układami na płytkach drukowanych pozuje do fotografii.
Zasilacz o napięciu wyjściowym 5V wykorzystujący scalony stablizator napięcia (UL7805). Widok schematu w programie KiCAD.
Znana i lubiana "Malinka". Prototypowy układ służący do sterowania urządzeniem zewnętrznym w zależności od aktualnej temperatury otoczenia. Aplikacja z GUI w języku Python.
System operayjny HAIKU OS: pulpit, oraz przykładowa aplikacja zliczająca kliknięcia ,w języku C++.
krótki przykład możliwości programowania w kodzie maszynowym mikroprocesora Z80 A CPU
Mikroprocesor posiada określony zestaw instrukcji które potrafi wykonać. Rozkazy Z80 są ciągiem ośmiobitowych liczb binarnych (kody maszynowe rozkazów). Każdy rozkaz jest złożeniem od 1 do 5 cykli maszynowych /OCF, MR, MW, PR, PW/. Działalność jednostki centralnej sprowadza się do pobierania i wykonywania ciągu rozkazów umieszczonych w pamięci zewnętrznej. Bezpośrednie operowanie na rozkazach mikroprocesora umożliwia programowanie komputera na poziomie elektroniki i pełną kontrolę jego działań.
Kod maszynowy jest ciągiem instrukcji (rozkazów) w postaci binarnej wykonywanych przez mikroprocesor.
Język Asemblera - jest językiem programowania którego każda instrukcja odpowiada dokładnie jednemu rozkazowi CPU, każdemu rozkazowi odpowiada mnemonik (symboliczny zapis rozkazu).
Asembler - to program dokonujacy asemblacji, czyli bezpośredniej translacji z kodu źródłowego w języku asemblera na wykonywalny kod maszynowy mikroprocesora.
MAXAM ASSEMBLER - translacja instrukcji asemblera i wykonanie kodu maszynowego z poziomu interpretera BASIC'a
MACRO-80 (macro assembler) - tworzenie kodu maszynowego w systemie operacyjnym CP/M

AMSTRAD CPC6128
komputer z mikroprocesorem Z80
SWOBODNA KOMPOZYCJA FOTOGRAFII Z RÓŻNYCH MIEJSC
ZATRZYMAJ SIĘ TU NA CHWILĘ - SUBIEKTYWNY WYBÓR MNIEJ LUB BARDZIEJ TRAFNYCH SENTENCJI
JEŻELI
Jeżeli zdołasz zachować spokój,
chociażby wszyscy go stracili, ciebie oskarżając;
Jeżeli nadal masz nadzieję, chociażby wszyscy o Tobie zwątpili,
licząc się jednak z ich zastrzeżeniem;
Jeżeli umiesz czekać bez zmęczenia,
jeżeli na obelgi nie reagujesz obelgami,
jeżeli nie odpłacasz na nienawiść nienawiścią,
nie udając jednakże mędrca i świętego;
Jeżeli marząc - nie ulegasz marzeniom;
Jeżeli rozumując - rozumowania nie czynisz celem;
Jeżeli umiesz przyjąć sukces i porażkę,
traktując jednakowo oba te złudzenia,
Jeżeli ścierpisz wypaczenie prawdy przez Ciebie głoszonej,
kiedy krętacze czynią z niej zasadzkę, by wydrwić naiwnych
albo zaakceptujesz ruinę tego, co było treścią twego życia,
kiedy pokornie zaczniesz odbudowę zużytymi już narzędziami;
Jeśli potrafisz na jednej szali położyć wszystkie twe sukcesy
i potrafisz zaryzykować, stawiając wszystko na jedną kartę,
jeśli potrafisz przegrać i zacząć wszystko od początku, bez słowa,
nie żaląc się, że przegrałeś;
Jeżeli umiesz zmusić serce, nerwy, siły, by nie zawiodły,
choćbyś od dawna czuł ich wyczerpanie,
byleby wytrwać, gdy poza wolą nic już nie mówi o wytrwaniu;
Jeżeli umiesz rozmawiać z nieuczciwymi, nie tracąc uczciwości
lub spacerować z królem w sposób naturalny,
Jeżeli nie mogą Cię zranić nieprzyjaciele ani serdeczni przyjaciele;
Jeżeli cenisz wszystkich ludzi, nikogo nie przeceniając;
Jeżeli potrafisz spożytkować każdą minutę,
nadając wartość każdej przemijającej chwili;
Twoja jest ziemia i wszystko, co na niej
i co - najważniejsze - synu mój - będziesz Mężczyzną
Rudyard Kipling
GDYBYM BYŁA BOGIEM...
Gdybym była Bogiem
płakałabym nad ludźmi
których stworzyłam
na swoje podobieństwo.
Jakżebym płakała nad ich złem
i podłością
i okrucieństwem
i głupotą
i ich nieszczęsną dobrocią
i bezradną rozpaczą i smutkiem.
I jakże bym płakała
nad każdym przedśmiertnym krzykiem
i cała krwią, która płynie nadaremnie
tak strasznie nadaremnie
i nad głodem
i beznadzieją
i nędzą
i wszystkimi szalonymi mękami
i samotną śmiercią
i nad torturowanymi,
którzy krzyczą i krzyczą
i nad torturującymi jeszcze bardziej.
I nad wszystkimi dziećmi
wszystkimi wszystkimi dziećm
nad nimi płakałabym najbardziej.
Tak, gdybym była Bogiem
to płakałabym nad nimi gorzko,
bo nie myślałam, że będzie im
tak jak jest.
Rzekami rzekami bym płakała
żeby mogli się potopić
w moich łez wielkiej wodzie
wszyscy biedni ludzie
i wreszcie
nastałby spokój.
Astrid Lindgren
Przytaczam fragmenty książki „Szczęście w przestrzeniach Banacha” autorstwa Michała Hellera wydanie z 1997 roku. Pozycja traktuje między innymi o filozofii przyrody, a także o nieliniowym modelu ewolucji samej nauki. Skupiłem się tylko na prezentacji kilku wyizolowanych z szerszej treści fragmentów przybliżających zagadnienia termodynamiki nieliniowej w powiązaniu z modelowaniem ewolucji form i procesów twórczych w przyrodzie. Prezentowane niżej treści zamieszczam z zamiarem zaciekawienia lekturą wymienionej książki, jak również zainteresowania tematyką samej filozofii nauki, w kontekście możliwości i próby opisania otaczającego nas świata przez nauki ścisłe.
„Widowisko wszechświata jest nieustannym ruchem narodzin, rozwoju, niszczenia form. Zadaniem wszystkich nauk jest przewidzieć tę ewolucję i jeżeli to możliwe wyjaśnić ją.”
Matematyczna teoria układów dynamicznych. Pojęcie układu dynamicznego powstaje w następującym kontekście. Gdy mamy do czynienia z jakimkolwiek układem fizycznym, musimy zacząć od opisania stanów, w jakich układ może się znajdować, czyli od określenia przestrzeni stanów. Bardzo często przestrzeń stanów ma strukturę rozmaitości. Następnym krokiem badania rozważanego układu jest określenie jego ewolucji, czyli ciągu stanów, jakie układ przyjmuje w czasie. Prowadzi to do równania różniczkowego zwyczajnego pierwszego stopnia określonego na rozmaitości stanów czyli pojęcia układu dynamicznego. Matematyczna analiza globalna to badanie stabilnych struktur w stanach odległych od równowagi termodynamicznej (termodynamika nieliniowa).
ZAŁOŻENIE PAŁACOWO-OGRODOWE
SIEDZIBA RODU BRANICKICH HERBU GRYF
Rozwój w XVIII wieku Białystok zawdzięcza dzięki hetmanowi Janowi Klemensowi Branickiemu.
To skromne w początkach XVIII wieku miasteczko stało się największym ośrodkiem pomiędzy Warszawą,
Wilnem, Grodnem i Lublinem.
Branicki, kasztelan krakowski, który miał przede wszystkim na względzie nadanie wielkopańskiego splendoru
własnej rezydencji,
dbał jednocześnie aby powiązane z nią miasto nie odstawało od wspaniałego charakteru
siedziby magnackiej i stanowiło jej godną oprawę.
Braniccy utworzyli w Białymstoku jedną z najświetniejszych rezydencji magnackich w ówczesnej Polsce.
Jakub Raczko Tabutowicz, któremu książę litewski Michał Zygmuntowicz, nadał puszczę porastającą dorzecze rzeki Białej
W 1547 roku Katarzyna Wołowiczówna, wdowa po ostatnim z Raczkowiczów, wyszła za mąż za Piotra Wiesiołowskiego herbu Ogończyk, wnosząc w posagu białostockie włości
W 1556 roku po śmierci Piotra następcą zostaje jego starszy syn Jan Wiesiołowski a po jego smieci w 1570 roku dobra przejął drugi syn, również Piotr, zwany dla odróżnienia od ojca Młodszym
Następcą Piotra Młodszego został jego syn Krzysztof, który odziedziczył białostockie dobra w 1621 r. Zmarł bezpotomnie w 1637 roku
Stefan Czarniecki
W 1659 r. tykocińskie starostwo wraz z Białymstokiem otrzymał własność za zasługi poniesione w wojnie ze Szwedami hetman Stefan Czarniecki i przekazał je córce Aleksandrze Katarzynie poślubionej w 1654 r. przez nadwornego marszałka koronnego, Jana Klemensa Branickiego (1624-1673)
Stefan Mikołaj Branicki
Syn Jana Klemensa i wnuk Stefana Czarnieckiego Stefan Mikołaj Branicki (1640-1709) po śmierci ojca w 1673 roku otrzymuje dobra białostockie. Zbudował w latach siedemdziesiątych XVII wieku dworską siedzibę. W latach 1691-1697 nastąpiła przebudowa dworu (który nosił cechy zamku obronnego) nadając budowli styl rezydencji barokowej
Jan Klemens Branicki (hetman wielki koronny)
W 1709 roku (umarł Stefan Mikołaj Branicki) dobra białostockie przejął syn Jan Kazimierz Branicki (1689-1771) który na cześć swojego dziada przyjął jego drugie imię Klemens. Od 1726 roku zaczął rozbudowywać białostocki pałac.
Śmierć Jana Klemensa Branickiego
W 1771 roku umiera Jan Klemens Branicki. Jego śmierć zahamowała rozbudowę pałacu i ogrodów. Wdowa po hetmanie, która otrzymała jedynie dożywocie, prowadziła jeszcze przez pewien czas prace upiększające pałacowy park
Zapis o sprzedaży Białostockiego Pałacu
Izabela branicka w 1802 roku sprzedała białostocki pałac królowi pruskiemu, z zastrzeżeniem, iż nie może zostać objęty za jej życia
(Król Prus nie objął go nigdy, gdyż po traktacie w Tylży (1807r.) Białostocczyzna znalazła się w granicach Rosji)
Aleksander I przejmuje Pałac
Po śmierci Izabeli (1808r.), białostocki pałac wraz z całym wyposażeniem przejął na swoją letnią rezydencję car Aleksander I
W 1692 roku podczas przebudowy dworu Stefana Mikołaja Branickiego, Tylman z Gameren zaprojektował ogrody do właśnie powstającego barokowego pałacu, lecz prawdziwie barkowe ogrody przy „Wersalu Podlaskim” zaczęto zakładać dopiero w 1732 r. na polecenie Jana Klemensa Branickiego.
Zespół pałacowo-ogrodowy Branickich tworzy zwarty kompleks rezydencji magnackiej pochodzącej z XVIII w.
Rezydencja składa się z pałacu wraz z ogrodami, zwierzyńcami i zabudowaniami.
Pałac otaczał geometryczny ogród założony z ośmiu kwater, powstał także kanał parkowy. W najszerszej części kanału pozostawiono wysepkę, którą obsadzono drzewami i nazwano „kępą”. Niedaleko znajdowała się przystań z której można było wyruszyć na przejażdżkę łódką.
W 1737 r. uformowano boskiety i szpalery w ogrodzie górnym i dolnym.
W 1738 r. na kanale, na osi ogrodu powstała fontanna ozdobiona rzeźbą jelenia. Pod koniec lat 30. XVIII w. zaplanowano zwierzyniec dla danieli i jeleni.
Powstały, także pawilony ogrodowe: Salon Włoski, Pawilon nad Kanałem oraz Pawilon Chiński.
W latach 1752-1756 postawiono i zdobiono Pawilon pod Orłem. W latach czterdziestych trwały prace wykończeniowe i dekoracyjne.
W latach 1752-1756 postawiono i zdobiono Pawilon pod Orłem. W 1752 roku taras ogrodowy otoczono kamienną balustradą.
Białostockie oranżerie słynęły w całej Polsce. W trzech budynkach przechowywano rośliny egzotyczne. W 1755 roku obok pomarańczarni wybudowano oddzielną figarnię. Ozdobnych drzew było ponad trzysta.
W skład założenia ogrodowego wchodziły między innymi:
odrobinę o sobie
Dość trafne będzie stwierdzenie ……….. dobra dusza którą cieszy wschód słońca każdego dnia.
Otwarcie mogę określić siebie jako miłośnika elektroniki, będącej wdzięcznym obiektem zainteresowań. Szczególnie z wcześniejszego nowatorsko-odkrywczego okresu, gdy kontakt z technologią wzbudzał fascynację i niepohamowaną ciekawość, a zgłębianie, konstruowanie i uruchamianie układów było samo w sobie przyjemnością i otwierało wrota wyobraźni.
Cechuje mnie zbiór wielu emocji, od zachwytu naturą po podziw dla głębi wszechświata. Dostrzegam niezwykły urok filozofii przyrody i analitycznego podejścia do świata. Z entuzjazmem traktuję osiągnięcia nauk przyrodniczych, a także odkrywanie historii minionych epok, ówczesnych społeczeństw, czy estetycznej oprawy życia.
Bliskie są mi dźwięki el-muzyki, do której przekonały mnie audycje Jerzego Kordowicza. Czerpię także radość z doświadczeń dźwiękowych bywając w filharmonii. Cenię inspirujące konwersacje i wnikliwe budzące ciekawość myślenie, czy też umilającą codzenność wrażliwość na dobra kultury.
Sportowe przyjemności realizuję grywając w tenisa.
Życzę wszystkim nieustannej ciekawości i rozkwitu twórczych inwencji. I jak w marzeniu, tym wyczekiwanym, pouczucia zadowolenia, radości, a może nawet euforii szczęśliwości.
Pochodzę i mieszkam w Białymstoku.
Bardzo mi przyjemnie że mogę Cię tu gościć.
Zapraszam do przeglądania zawartości witryny.
